www.hanno-rein.de | Software | Worldlight
Worldlight
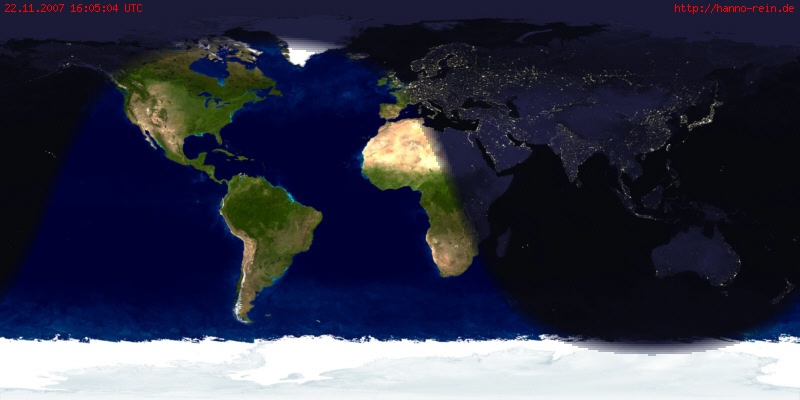
Das Bild zeigt die aktuelle Tag/Nacht Grenze auf der Erde. Das langsame Überblenden von hell nach dunkel simuliert die bürgerliche Dämmerung. Die zwei Rohbilder stammen von
Reto Stockli
und dem BlueMarble Projekt des Nasa Earth Observatory.
Mein Skript errechnet nun zu jedem Punkt auf der Erde den aktuellen Winkel, unter dem die Sonne zu sehen ist. Dies geschieht
hauptsächlich durch Rotationen des Koordinatensystems.
Dadurch braucht man nur sehr wenige Daten um den aktuellen Sonnenstand zu berechnen:
 Datum und Uhrzeit (UTC)
Datum und Uhrzeit (UTC)
 Breiten und Längengrad (die verwendete Karte hat ein orthogonales Koordinatensystem)
Breiten und Längengrad (die verwendete Karte hat ein orthogonales Koordinatensystem)
 21. Juni ist Sommersonnenwende
21. Juni ist Sommersonnenwende
 12 Uhr Mittags ist Kulmination der Sonne
12 Uhr Mittags ist Kulmination der Sonne
Das Koordinatensystem (x,y,z) wird nun so gelegt, dass die Erde im Zentrum ist und die Sonne sich in positiver
x-Richtung befindet. Die x-y-Ebene sei die Ekliptik. Zunächst wird anhand der Uhrzeit (wahre Ortszeit), der geographischen Länge und Breite der
Vektor r berechnet, der senkrecht zur Erdoberfläche stehen würde, wenn die Erdachse nicht gekippt wäre.
Die Erddrehachse rotiert nun allerdings in diesem Koordinatensystem einmal im Jahr um die z-Achse. Um den Vektor r in Abhängigkeit von der Jahreszeit zu drehen,
wird eine Drehmatrix benötigt, die um eine beliebige Achse in der x-y-Ebene drehen kann.
Die Drehachse ist genau jene, die auf der Erdachse und der x-Achse senkrecht steht. Der Drehwinkel ist 23.5 Grad.
Ist der x-Wert des Vektors nun positiv, so ist die Sonne für den Beobachter über dem Horizont.
Rechnet man mit Hilfe des Skalarprodukts den Winkel zwischen Sonne und Vektor r aus,
so lassen sich auch die verschiedenen Dämmerungen (bürgerliche, astronomische, nautische) simulieren.
Das Skript wurde vollständig in PHP geschrieben und wird regelmäßig alle zwei Minuten ausgeführt, um die neuesten Bilder zu berechnen.
Quelltext:
<?
// Wieviel Uhr?
$ts = strtotime("now");
// Berechne einige Konstanten im Voraus:
// Zeitgleichung in Minuten
$zg = 1*3600*(-0.1752*sin(0.033430 * gmdate("z",$ts) + 0.5474) - 0.1340*sin(0.018234*gmdate("z",$ts) - 0.1939));
if ($zg<0){
$ts=strtotime("now ".(int)$zg." second",$ts);
}else{
$ts=strtotime("+ ".(int)$zg." second",$ts);
}
// Jahr und Tag berechnen (zwischen 0 und 2 Pi)
$tagg = ((gmdate("H",$ts)*60+gmdate("i",$ts))*60+gmdate("s",$ts))/43200*pi();
$jahr = (gmdate("z",$ts)-79.25)/365*2*pi();
// Erdachse steht um 23.5° schief:
$alpha= 0.41015237422;
$cosalpha = cos($alpha);
$sinalpha = sin($alpha);
$cosjahr = cos($jahr);
$sinjahr = sin($jahr);
// Berechne Winkel, under dem die Sonne zu sehen ist
function angle($l,$b){
// Breite b und Länge l werden in Grad erwartet
global $tagg, $cosalpha, $sinalpha, $cosjahr, $sinjahr;
// Bogenmaßumrechnung
$b = (90-$b)/180*pi();
$tag = $tagg-$l/180*pi();
// Zenitvektor an der Oberfläche ohne schiefe Erdachse
// Sonne steht in Richtung der positiven x-Achse, Erdrotation noch in Richtung der z-Achse
$sinb = sin($b);
$r = array(-1*cos($tag)*$sinb,sin($tag)*$sinb,cos($b));
// Erdachse dreht sich zusätzlich im Verlauf des Jahres, darum die etwas
// komplizierte Drehmatrix um eine beliebige Drehachse r mit z=0 und |r|=1
//$matrix = array(array((1-cos($alpha))*cos($jahr)*cos($jahr)+cos($alpha) ,
// (1-cos($alpha))*cos($jahr)*sin($jahr),
// -1*sin($alpha)*sin($jahr)),
// array((1-cos($alpha))*cos($jahr)*sin($jahr),
// (1-cos($alpha))*sin($jahr)*sin($jahr)+cos($alpha),
// (1-cos($alpha))*cos($jahr)*sin($jahr)),
// array(sin($alpha)*sin($jahr),
// -1*sin($alpha)*cos($jahr),
// cos($alpha)));
// Führe Drehung aus (berechne nur den wichtigen x-Wert:
return $r[0] * ((1-$cosalpha)*$cosjahr*$cosjahr+$cosalpha)
+ $r[1] * (1-$cosalpha)*$cosjahr*$sinjahr
- $r[2] * $sinalpha*$sinjahr;
}
// Einlesen der Bilder aus Dateien:
$inputfile_day = "./land_ocean_ice_800.jpg";
$inputfile_night= "./land_ocean_ice_lights_800.jpg";
$size = getimagesize($inputfile_day);
$im = imagecreatefromjpeg($inputfile_day);
$im2 = imagecreatefromjpeg($inputfile_night);
$col = imagecolorallocate($im,255,0,0);
$col2 = imagecolorallocate($im,55,55,55);
// Pixelgröße (je kleiner, desto langsamer)
$blocksize = 2;
for($i=0;$i<$size[0];$i=$i+$blocksize){
for($j=0;$j<$size[1];$j=$j+$blocksize){
$x = angle(180-($i/$size[0]*360),-90+($j/$size[1]*180));
if ($x<-0.11){
ImageCopy($im,$im2,$i,$j,$i,$j,$blocksize,$blocksize);
}elseif($x<0){
$offset = 13;
$ptc = (int)(100-($x+0.11)/(0.11)*(100-$offset))+$offset;
if($ptc>100){$ptc=100;}
ImageCopyMerge($im,$im2,$i,$j,$i,$j,$blocksize,$blocksize,$ptc);
}
}
}
// Ausgabe in Datei:
$im3 = imagecreatetruecolor(800,100);
imagecopy($im3,$im,0,0,0,50,800,100);
imagestring($im,2,5,1,gmdate("d.m.Y H:i:s ")."UTC",$col);
imagestring($im,2,675,1,"hanno-rein.de",$col);
ImageJPEG ($im,"../worldlight_800.jpg",95);
ImageJPEG ($im3,'',90);*/
ImageJPEG ($im3,"../worldlight_start.jpg",90);
?>
Sollten Sie Fragen haben, zögern Sie nicht mir zu schreiben.
http://www.hanno-rein.de/software/12/?printable=true
(c) Hanno Rein 2020